本专栏用于记录关于深度学习的笔记,不光方便自己复习与查阅,同时也希望能给您解决一些关于深度学习的相关问题,并提供一些微不足道的人工神经网络模型设计思路。
专栏地址:「深度学习一遍过」必修篇
目录
1?优化器的高级使用
1.1 基于更新方向
1.1.1?随机梯度下降?SGD 优化算法
1.1.2?momentum 动量法?
1.1.3?Nesterov accelerated gradient 法
1.2?基于选择更为合理的学习率
1.2.1 Adam 优化算法
1.2.2?RMSprop 优化算法
1.2.3 Adadelta优化算法
1.2.4 Adagrad优化算法
1.2.5 Adamax优化算法
1.2.6 AMSgrad 方法
2 学习率迭代策略
2.1 StepLR调整算法
2.2 MultiStepLR 调整算法
2.3 ExponentialLR
2.4?LambdaLR
3 分类优化目标定义
3.1?NLLLoss优化目标
3.2 CrossEntropyLoss优化目标
3.3?BCELoss优化目标
3.4?KL散度优化目标:
3.5?MSELoss与L1优化目标
实例补充:损失函数
L1Loss?
MSELoss
交叉熵损失
反向传播
为每个参数单独设置选项:
 的参数将会使用
的参数将会使用  的学习率,
的学习率, 的参数将会使用
的参数将会使用  的学习率,并且
的学习率,并且  的
的  ?将会被用于所有的参数。
?将会被用于所有的参数。
梯度下降算法中,学习率太大,函数无法收敛,甚至发散,如下图。学习率足够小,理论上是可以达到局部最优值的(非凸函数不能保证达到全局最优),但学习率太小却使得学习过程过于缓慢,合适的学习率应该是能在保证收敛的前提下,能尽快收敛。对于深度网络中,参数众多,参数值初始位置随机,同样大小的学习率,对于某些参数可能合适,对另外一些参数可能偏小(学习过程缓慢),对另外一些参数可能太大(无法收敛,甚至发散),而学习率一般而言对所有参数都是固定的,所以无法同时满足所有参数的要求。通过引入 ?可以让那些因学习率太大而来回摆动的参数,梯度能前后抵消,从而阻止发散。?
?可以让那些因学习率太大而来回摆动的参数,梯度能前后抵消,从而阻止发散。?
1.1.1?随机梯度下降?SGD 优化算法
 (
( ) – 待优化参数的
) – 待优化参数的  或者是定义了参数组的
或者是定义了参数组的 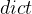
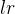 (
( ) – 学习率
) – 学习率  (
( , 可选) – 动量因子(默认:
, 可选) – 动量因子(默认: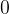 )
)  (
( , 可选) – 权重衰减(
, 可选) – 权重衰减( 惩罚)(默认:
惩罚)(默认: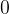 )
)  (
( , 可选) – 动量的抑制因子(默认:
, 可选) – 动量的抑制因子(默认: )
)  (
( , 可选) – 使用
, 可选) – 使用  ?动量(默认:
?动量(默认: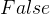 )
)
在某多分类任务中,设置其损失函数、优化器、学习率:

我们可视化后发现,训练集和测试集整体的正确率是呈现上升趋势,训练集的  ?呈现下降趋势也没问题,但测试集的
?呈现下降趋势也没问题,但测试集的  ?呈现突然地暴涨而无法收敛,于是我们断定选用
?呈现突然地暴涨而无法收敛,于是我们断定选用  优化算法,尤其是填入的这几个参数无法阻止模型梯度发散,所以决定换个优化算法试试,具体见下文。
优化算法,尤其是填入的这几个参数无法阻止模型梯度发散,所以决定换个优化算法试试,具体见下文。
1.1.2?momentum 动量法?
加速SGD,特别是处理高曲率、小但一致的梯度;积累了之前梯度指数级衰减的移动平均,并且继续沿该方向移动。?

如果梯度方向不变,就越发更新的快,反之减弱,当前保证梯度收敛。?
1.1.3?Nesterov accelerated gradient 法
在标准动量方法中添加了一个校正因子?

要求梯度下降更快,更加智能,直接先按照前一次梯度方向更新一步将它作为当前的梯度?
1.2.1 Adam 优化算法
对梯度的一阶和二阶都进行了估计与偏差修正,使用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。
优点:
- 对学习率没有那么敏感,学习步长有一个确定 的范围,参数更新比较稳。
缺点:
- 学习率在训练的后期仍然可能不稳定导致无法 收敛到足够好的值,泛化能力较差。
 (
( ) – 待优化参数的iterable或者是定义了参数组的?
) – 待优化参数的iterable或者是定义了参数组的?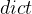
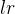 ?(
?( , 可选) – 学习率(默认:
, 可选) – 学习率(默认: )
)  ?(
?( ?[
?[ ,
,  ], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认:
], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数(默认: ,
, )
)  ?(
?( , 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:
, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认: )
)  ?(
?( , 可选) – 权重衰减(
, 可选) – 权重衰减( ?惩罚)(默认:
?惩罚)(默认: 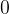 )
)
在某多分类任务中,设置其损失函数、优化器、学习率:

还是同样的结果:验证集的  ?又没有收敛,于是我果断提前按下了 “暂停” 键。此情此景下,我分析:改了个优化器不行,于是我决定进行调参这一痛苦操作…………
?又没有收敛,于是我果断提前按下了 “暂停” 键。此情此景下,我分析:改了个优化器不行,于是我决定进行调参这一痛苦操作…………
1.2.2?RMSprop 优化算法
 (
( ) – 待优化参数的
) – 待优化参数的  ?或者是定义了参数组的?
?或者是定义了参数组的?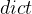
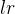 (
( , 可选) – 学习率(默认:
, 可选) – 学习率(默认: )
)  (
( , 可选) – 动量因子(默认:
, 可选) – 动量因子(默认: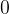 )
)  (
( , 可选) – 平滑常数(默认:
, 可选) – 平滑常数(默认: )
)  ?(
?( , 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:
, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认: )
)  ?(
?( , 可选) – 如果为
, 可选) – 如果为 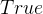 ,计算中心化的
,计算中心化的  ,并且用它的方差预测值对梯度进行归一化
,并且用它的方差预测值对梯度进行归一化  (
( , 可选) – 权重衰减(
, 可选) – 权重衰减( ?惩罚)(默认:
?惩罚)(默认: 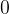 )
)
1.2.3 Adadelta优化算法
1.2.4 Adagrad优化算法
自适应地为各个维度的参数分配不同的学习率?
优点:
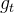 ?较小的时候,能够放大梯度,较大的时候,能够约束梯度(激励+惩罚)。
?较小的时候,能够放大梯度,较大的时候,能够约束梯度(激励+惩罚)。
缺点:
- 梯度累积导致学习率单调递减,后期学习率非常小。
- 需要设置一个合适的全局初始学习率 。
 ?(
?( ) – 待优化参数的?
) – 待优化参数的? ?或者是定义了参数组的?
?或者是定义了参数组的?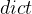
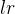 (
( , 可选) – 学习率(默认:
, 可选) – 学习率(默认:  )
)  (
( , 可选) – 学习率衰减(默认:
, 可选) – 学习率衰减(默认: 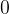 )
)  (
( , 可选) – 权重衰减(
, 可选) – 权重衰减( ?惩罚)(默认:
?惩罚)(默认: 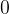 )
)
1.2.5 Adamax优化算法
 ?(
?( ) – 待优化参数的
) – 待优化参数的  ?或者是定义了参数组的?
?或者是定义了参数组的?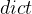
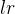 (
( , 可选) – 学习率(默认:
, 可选) – 学习率(默认: )
)  ?(
?( ?[
?[ ,
,  ], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数
], 可选) – 用于计算梯度以及梯度平方的运行平均值的系数  ?(
?( , 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认:
, 可选) – 为了增加数值计算的稳定性而加到分母里的项(默认: )
)  (
( , 可选) – 权重衰减(
, 可选) – 权重衰减( ?惩罚)(默认:
?惩罚)(默认: 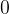 )
)
1.2.6 AMSgrad 方法
Adam 类的方法之所以会不能收敛到好的结果,是因为在优化算法中广泛使用的指数衰减方法会使得梯度的记忆时间太短。
使用过去平方梯度的最大值来更新参数, 而不是指数平均 。
等间隔调整学习率,调整倍数为  ?倍,调整间隔为
?倍,调整间隔为  ,
,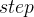 ?指
?指  。
。
调节的  ?是自己定义。
?是自己定义。
指数形式增长
能够根据自己的定义调节?
机器学习用有限训练集上的期望损失作为优化目标(代理损失函数 ),损失代表预测值
),损失代表预测值 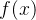 ?与真实值
?与真实值 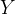 ?的不一致程度,损失函数越小,一般模型的性能越好。
?的不一致程度,损失函数越小,一般模型的性能越好。
观察训练集和测试集的误差就能知道模型的收敛情况,估计模型的性能。
选择合适的优化目标
改进优化目标

通过

包来构建
 ?散度常用来描述两个分布的距离,并在输出分布的空间上执行直接回归是有用的。
?散度常用来描述两个分布的距离,并在输出分布的空间上执行直接回归是有用的。
 ?应该和
?应该和  ?的形状相同
?的形状相同
- 计算实际输出和目标之间的差距
- 为我们更新输出提供一定的依据(反向传播)?
L1Loss?

MSELoss

交叉熵损失

反向传播

感谢阅读
END

?可以让那些因学习率太大而来回摆动的参数,梯度能前后抵消,从而阻止发散。?

?呈现下降趋势也没问题,但测试集的
?呈现突然地暴涨而无法收敛,于是我们断定选用
优化算法,尤其是填入的这几个参数无法阻止模型梯度发散,所以决定换个优化算法试试,具体见下文。



?又没有收敛,于是我果断提前按下了 “暂停” 键。此情此景下,我分析:改了个优化器不行,于是我决定进行调参这一痛苦操作…………
?倍,调整间隔为
,
?指
。
?是自己定义。
),损失代表预测值
?与真实值
?的不一致程度,损失函数越小,一般模型的性能越好。

损失,用于训练一个
?类分类器。
?和
?集成到一个类中
?与
?之间的二进制交叉熵
?散度常用来描述两个分布的距离,并在输出分布的空间上执行直接回归是有用的。



