本文采用深度确定性策略梯度 (DDPG) 算法实现无人机路径规划方法，建立了一个带有静态障碍物的环境，使无人机能够在三维连续环境下完成路径规划。

标题：A UAV Path Planning Method Based on Deep Reinforcement Learning

日期：2020

作者：Yibing Li, Sitong Zhang, Fang Ye*, Tao Jiang, Yingsong Li

期刊：2020 IEEE USNC-CNC-URSI North American Radio Science Meeting (Joint with AP-S Symposium)

无人机路径规划是救援行动的关键组成部分。由于受任务空间连续性和飞行器高动态特性的影响，传统的控制方法无法找到最优控制策略。为此，本文提出了一种基于深度强化学习 (DRL) 的无人机路径规划方法，使无人机能够在三维连续环境下完成路径规划。采用深度确定性策略梯度 (DDPG) 算法实现无人机自主决策。此外，为了避免障碍，提出了连通面积和威胁函数的概念，并将其应用于奖励函数中。最后，建立了一个带有静态障碍物的环境，并利用所提出的方法对无人机进行了训练。实验证明，该算法能够适应多种场景。

无人机的状态是由位置、速度和加速度定义的。无人机在 时刻的运动状态定义如下：

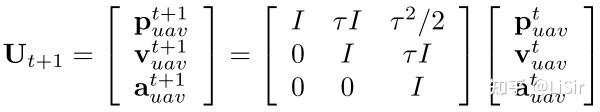
代表 时刻无人机的位置； 代表速度； 代表加速度；

和 ，分别代表无人机的偏角和俯仰角；

无人机旨在与障碍物保持距离，到达目标区域。

首先，为了引导无人机到达目标区域，将与无人机到目标点距离有关的奖赏函数 表示如下：

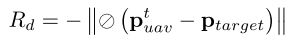
其中， 代表归一化； 代表 L2 正则化； 代表目标点的坐标。无人机离目标点越远，负奖励越大。

其次，为了与障碍物保持一定的距离，定义了一个威胁函数 ，表示障碍物对路径规划的威胁程度。

任务空间的示意图如图 b 所示。从图中可以看出，障碍物 1 和 2 与无人机的距离相同，但它们对路径规划任务的威胁程度不同。障碍 2 对任务的威胁明显更大。

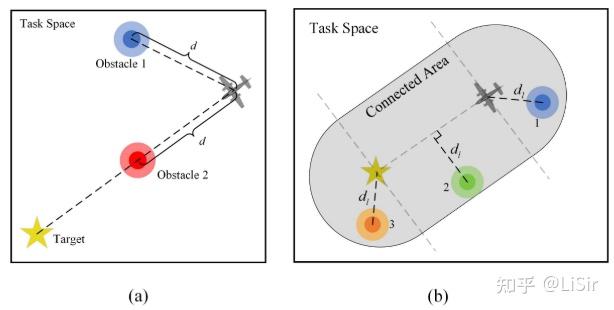
当障碍物位于位置1时， 为障碍物到无人机的距离；当位于位置2时， 为障碍物到无人机与目标点形成的线段的距离；当位于位置3时， 等于障碍物到目标点的距离。

威胁函数的定义如下。将 T 的负值作为无人机接近障碍物的惩罚。构造奖励函数

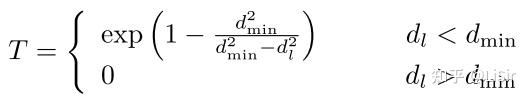
在数学上，路径规划问题可以表述为马尔可夫决策问题 (MDP)。DDPG是一种求解MDP问题的无模型算法，即决策过程与系统动力学无关。

我们设计了反映目标相关信息的特征 。 此外，为了加快DRL的收敛速度，我们对其进行了归一化处理。

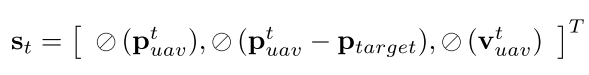
奖赏是强化学习的临界点之一，它在很大程度上决定了算法的性能。本研究设计了一个奖励函数，引导无人机到达目标区域，同时保证其安全性。

所提出的方法是在有静态障碍物的环境中训练的。无人机的任务空间是长方体，长15公里（从-7.5公里到7.5公里），宽15公里（从-7.5公里到7.5公里），高7.5公里（从0.5公里到8公里）。障碍和威胁区域简化为球体。在每一次事件中，目标点和障碍物呈现随机位置。

不同训练环境下累积奖励的平滑曲线如图a所示。 该图显示，网络在障碍物数为5、10和15时收敛。 用该方法规划的最优轨迹如图b所示。 从图中可以看出，该方法能够引导无人机成功避障，且路径短。

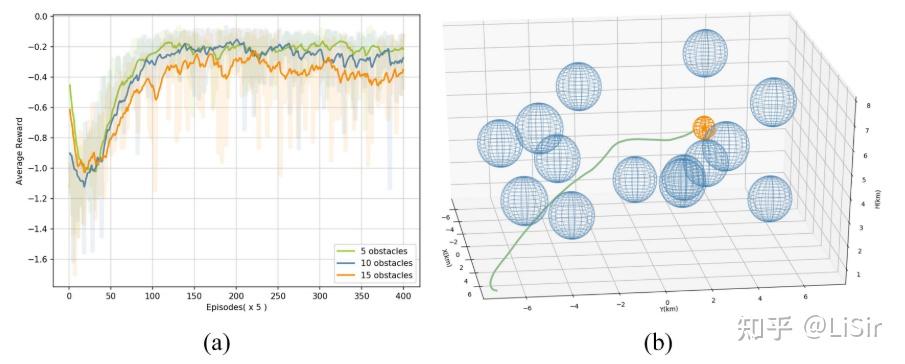
(a) 用所提议的方法平滑从一系列静态情况中获得的累积奖励曲线； (b)拟议方法规划的最佳轨迹图（橙色球体、蓝色球体和绿线代表目标区、威胁区和无人机路径）。