
卷积运算
卷积运算在图像滤波、深度学习、人工神经网络等领域被广泛使用,在图像处理中用矩阵卷积运算来进行滤波,起到特征提取的作用。这里主要介绍矩阵的卷积运算,即二维离散卷积。
运算过程如下

对应窗口矩阵元素逆序相乘并相加,作为卷积后的值。在图像处理中让窗口kernel滑动,逐一完成卷积运算
一般的卷积算法
实现卷积运算最朴素的方法是采用滑动窗口遍历矩阵,在边缘检测的滤波过程中实现过这个方法,
pizh12thu:图像算法在数值计算中的应用(1):Canny边缘检测算法这样会引入串行for循环逐一像素进行操作,然后在每一个窗口大小的矩阵上进行卷积运算,效率太低。下面扩展到3通道卷积操作,利用numpy切片同时计算3个通道。
def convolve2d(arr, kernel, stride=1, padding='same'):
'''
Using convolution kernel to smooth image
Parameters
=========== arr: 3D array or 3-channel image
kernel: Filter matrix
stride: Stride of scanning
padding: padding mode
'''
h, w, channel = arr.shape
k = kernel.shape[0]
r = int(k/2)
kernel_r = np.rot90(kernel,k=2,axes=(0,1))
# padding outer area with 0
padding_arr = np.zeros([h+k-1,w+k-1,channel])
padding_arr[r:h+r,r:w+r] = arr
new_arr = np.zeros(arr.shape)
for i in range(r,h+r,stride):
for j in range(r,w+r,stride):
roi = padding_arr[i-r:i+r+1,j-r:j+r+1]
new_arr[i-r,j-r] = np.sum(np.sum(roi*kernel_r,axis=0),axis=0)
return new_arr[::stride,::stride]构造小型数组进行简单的速度测试
if __name__=='__main__':
A = np.arange(1,10001).reshape((100,100,1))
print(A.shape)
kernel = np.arange(1,10).reshape((3,3,1))/45
# convert to 3-channels
A3 = np.concatenate((A, 2*A, 3*A), axis=-1)
k3 = np.concatenate((kernel, kernel, kernel), axis=-1)
t1 = time.time()
for i in range(100):
A1 = convolve2d(A3,kernel,stride=2).astype(np.int)
t2 = time.time()
print(t2-t1)
###output
(100, 100, 1)
3.2025175虽然不用循环计算多个通道,单通道与多通道耗时相同,但是依然需要for循环来滑动窗口kernel,对于大图片速度很慢,需要进一步将外层循环替代。
向量化索引运算
注意到for循环之间的代码是可以独立计算的,即不依赖上一步i、j计算的结果,那么就可以将这部分代码并行化,采用numpy的向量化操作进一步提升速度。将窗口中心点扫掠过的原图的坐标点(索引值)提取出来,组成向量vector,vector的每个元素是一个元组或数组,存储为 ,然后传入map进行多线程运算。生成坐标向量的方法就是计算笛卡尔积,得到所有可能的有序排列,假设集合
,集合
,则两个集合的笛卡尔积为
在python中,利用itertools.product计算可迭代对象的笛卡尔积。np.vectorize把函数向量化,但是并没有带来显著的速度提升,这里的切片视图操作速度快但是并没有产生新的内存数据,所以并没有产生预期的向量并发操作,内部还是按照for循环进行的。
def convolve2d_vector(arr, kernel, stride=1, padding='same'):
h, w, channel = arr.shape[0],arr.shape[1],arr.shape[2]
k = kernel.shape[0]
r = int(k/2)
kernel_r = np.rot90(kernel,k=2,axes=(0,1))
# padding outer area with 0
padding_arr = np.zeros([h+k-1,w+k-1,channel])
padding_arr[r:h+r,r:w+r] = arr
new_arr = np.zeros(arr.shape)
vector = np.array(list(itertools.product(np.arange(r,h+r,stride),np.arange(r,w+r,stride))))
vi = vector[:,0]
vj = vector[:,1]
def _convolution(vi,vj):
roi = padding_arr[vi-r:vi+r+1,vj-r:vj+r+1]
new_arr[vi-r,vj-r] = np.sum(np.sum(roi*kernel_r,axis=0),axis=0)
vfunc = np.vectorize(_convolution)
vfunc(vi,vj)
return new_arr[::stride,::stride]看来简单地使用 np.vectorize()并没有实现向量化展开,必须对原图的存储结构进行重新排列和扩展才能真正地利用向量化机制,即将窗口滑动转换为真正的矩阵运算。
矩阵乘法运算
正常的三通道卷积
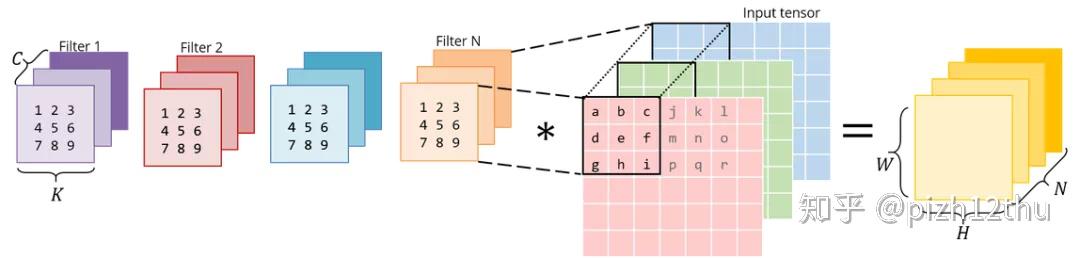
转换为矩阵相乘,对kernel和原图进行重新排列:
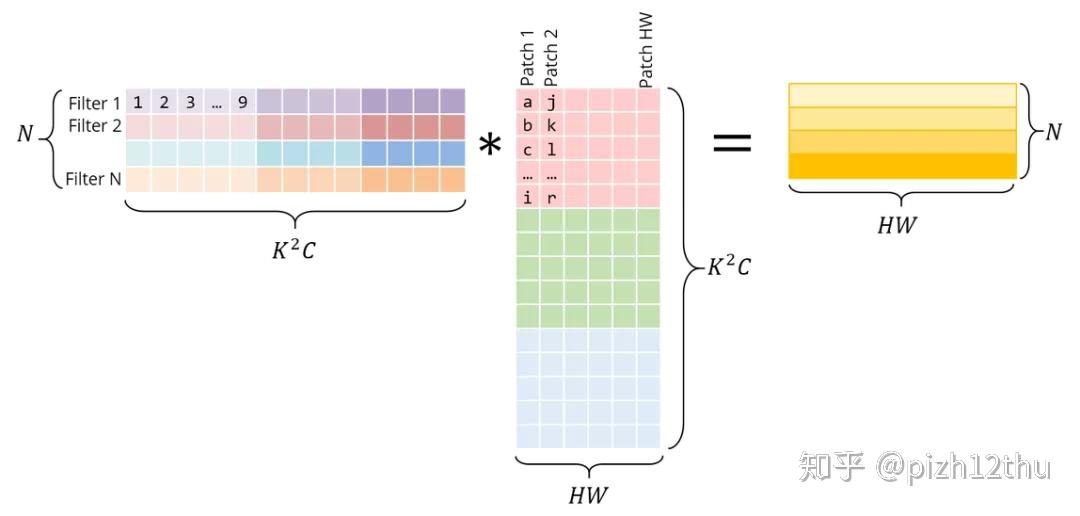
将卷积运算转化为矩阵乘法,从乘法和加法的运算次数上看没什么差别,但是转化成矩阵后,可以在连续内存和缓存上操作,而且有很多库提供了高效的实现方法(BLAS、MKL),numpy内部基于MKL实现运算的加速。图像展开消耗了更多的内存,以空间换时间,另一方面,展开成矩阵形式可以转换成CUDA代码使用GPU加速。
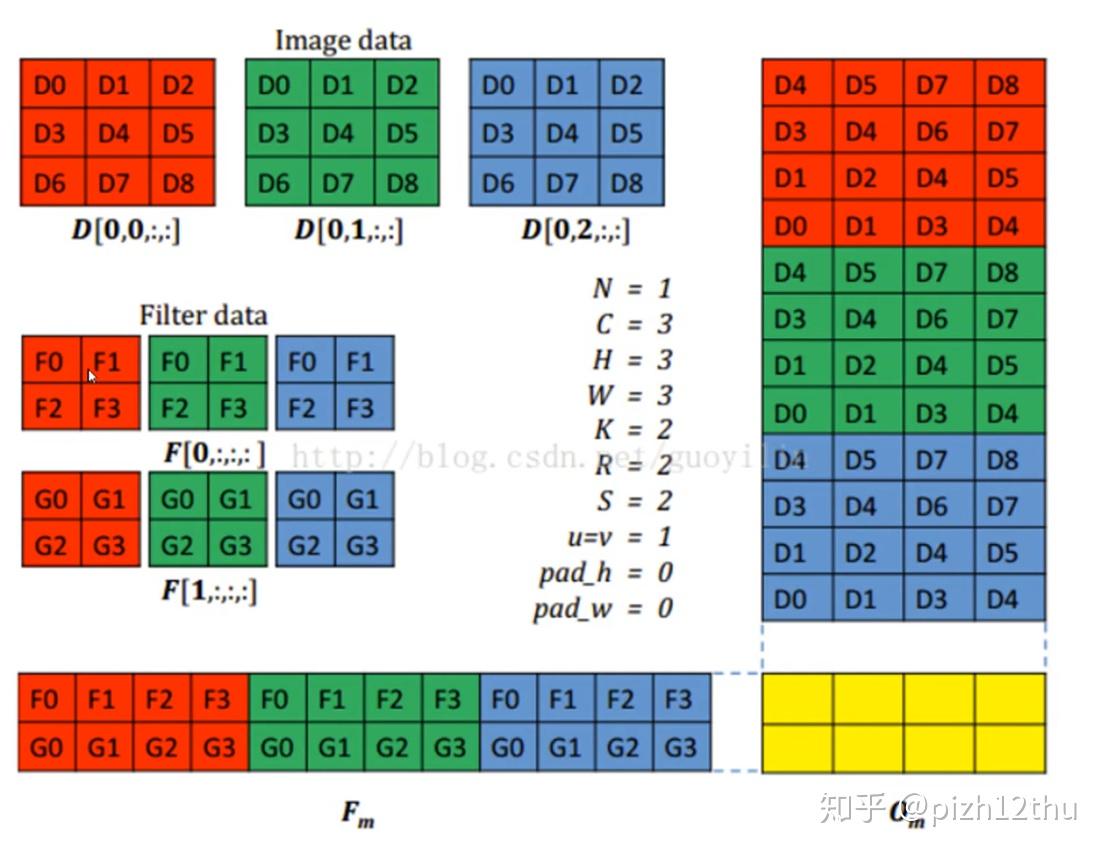
上图展示了3通道卷积的展开过程,RGB通道首位拼接,矩阵乘法运算后的结果是三个通道卷积结果的累加,这里有所不同,我们需要单独输出每个通道的卷积结果而不累加,与原图像大小相同,见下图。
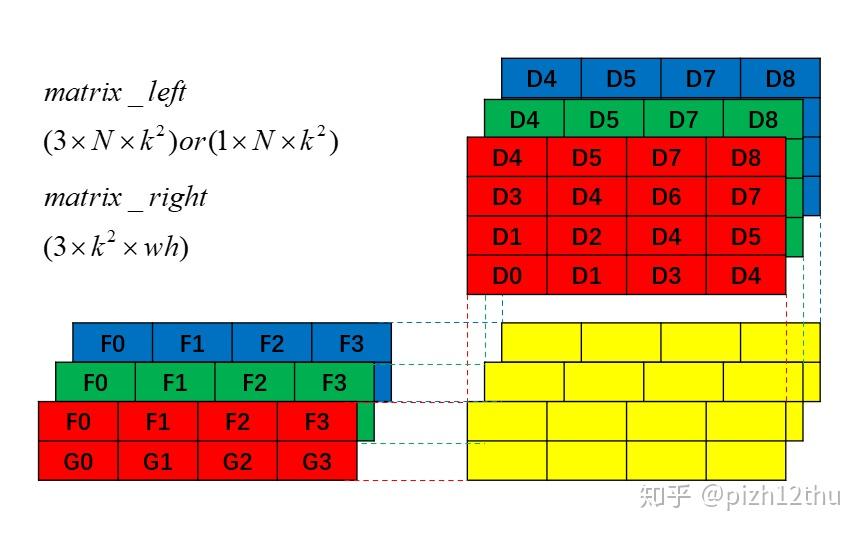
二维矩阵乘法采用np.dot()函数,而高维数组乘法运算采用np.matmul()函数。高维数组(n>2)相乘须满足以下两个条件:
两个n维数组的前n-2维必须完全相同。例如(3,2,4,2)(3,2,2,3)前两维必须完全一致;
最后两维必须满足二阶矩阵乘法要求。例如(3,2,4,2)(3,2,2,3)的后两维可视为(4,2)x(2,3)满足矩阵乘法。
先利用reshape将kernel展开为(1,k*k,c),再用转置函数transpose将channel前置,照此方法循环展开image矩阵。numpy的广播规则会将kernel的第一个维度补齐,所以输入kernel可以是1通道的(三通道共用一个卷积核)。
def convolve2d_vector(arr, kernel, stride=1, padding='same'):
h, w, channel = arr.shape[0],arr.shape[1],arr.shape[2]
k, n = kernel.shape[0], kernel.shape[2]
r = int(k/2)
#重新排列kernel为左乘矩阵,通道channel前置以便利用高维数组的矩阵乘法
matrix_l = kernel.reshape((1,k*k,n)).transpose((2,0,1))
padding_arr = np.zeros([h+k-1,w+k-1,channel])
padding_arr[r:h+r,r:w+r] = arr
#重新排列image为右乘矩阵,通道channel前置
matrix_r = np.zeros((channel,k*k,h*w))
for i in range(r,h+r,stride):
for j in range(r,w+r,stride):
roi = padding_arr[i-r:i+r+1,j-r:j+r+1].reshape((k*k,1,channel)).transpose((2,0,1))
matrix_r[:,:,(i-r)*w+j-r:(i-r)*w+j-r+1] = roi[:,::-1,:]
result = np.matmul(matrix_l, matrix_r)
out = result.reshape((channel,h,w)).transpose((1,2,0))
return out[::stride,::stride]用1000*1000大小的图像测试
if __name__=='__main__':
N=1000
A = np.arange(1,N**2+1).reshape((N,N,1))
print(A.shape)
kernel = np.arange(3**2).reshape((3,3,1))/45
# convert to 3-channels
A3 = np.concatenate((A, 2*A, 3*A), axis=-1)
k3 = np.concatenate((kernel, kernel, kernel), axis=-1)
t1 = time.time()
for i in range(1):
B1 = convolve2d(A,kernel,stride=2).astype(np.int)
t2 = time.time()
print(t2-t1)
t1 = time.time()
for i in range(1):
B2 = convolve2d_vector(A,kernel,stride=2).astype(np.int)
t2 = time.time()
print(t2-t1)
print(B1.all()==B2.all())
###output
(1000, 1000, 1)
4.517540216445923
0.8763346672058105
True可以看到运算结果与convolve2d滑动卷积的结果一致,且速度提升了5倍左右。速度主要瓶颈还是来自image的展开操作,这里还是滑动窗口扫描实现的,for循环内部进行了局部拷贝操作,是串行的,数组切片和矩阵运算部分是并行的。
总结
在CPU程序上优化卷积运算,numpy库是个不错的选择,初始算法将三通道计算和求和过程并行化,获得了接近3倍的加速。转换为矩阵/多维数组乘法后,速度进一步提升了5倍。在python中用多线程和多进程的方式加速for循环效果并不理想,CPU程序上创建和启动多线程开销很大,进程和线程通信、传递数据消耗了大部分时间,总体速度不升反降。