车辆路径问题（Vehicle Routing Problem，VRP）

来源：网络时间：2024-08-26 05:25

车辆路径问题（Vehicle Routing Problem，VRP）是一类经典的组合优化问题，涉及如何有效地分配一组车辆去访问多个客户点，并在满足约束条件的情况下最小化总行驶距离或成本。VRP在物流、配送、运输等领域有广泛的应用，以下是一些常见的VRP变体：

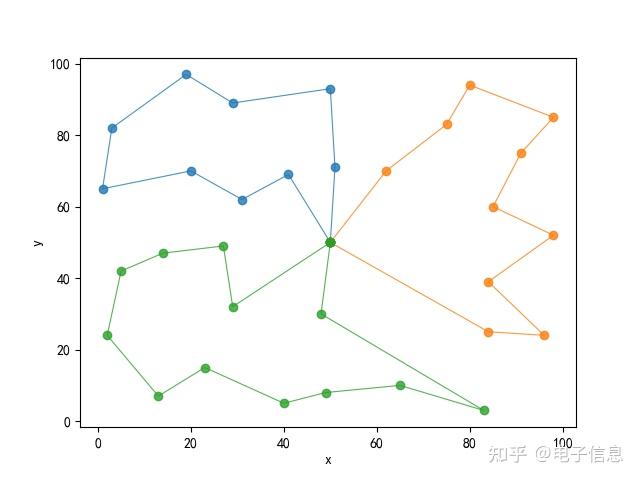
给定一组客户点、车辆容量、车辆数量、起始点和终点，目标是找到使得所有客户点都被访问一次的最短路径方案。基本车辆路径问题（Vehicle Routing Problem，VRP）的数学模型可以使用整数线性规划（Integer Linear Programming，ILP）来表示。以下是一个简化的VRP模型示例：

参数：

$n$ : 客户点的数量（不包括起始点）。
$m$ : 车辆的数量。
$c_{i,j}$ : 客户点 $i$ 到客户点 $j$ 的距离或成本。

变量：

$x_{i,j}^{k}$ : 若车辆 $k$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{i,j}^{k}$ 为1，否则为0。

目标函数：

最小化总行驶距离或成本： $Min\\sum_{k=1}^{m}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{i,j}\\cdot x_{ij}^{k}}}}\\\\$ 约束条件：

每个客户点必须被访问且仅被访问一次：

$\\sum_{k=1}^{m}{\\sum_{j=1}^{n}{x_{ij}^{k}}}=1,\\forall i=1,...n\\\\$ 2.每辆车的路径必须从起始点开始，并在终点结束：

$\\sum_{j=1}^{n}{x_{0j}^{k}}=1,\\forall k=1,...m\\\\$

$\\sum_{i=1}^{n}{x_{i0}^{k}}=1, \\forall k=1,...m\\\\$ 3.Binary(0-1)约束：

$x_{ij}^{k}\\in\\left\\{ 0,1\\right\\},\\forall i=0,...,n, \\forall j=0,...,n, \\forall k=0,...,m\\\\$ 该数学模型描述了不受容量约束的基本车辆路径问题（VRP）的数学规划形式，其中车辆可以无视容量限制，但仍需要找到使得总行驶距离或成本最小化的路径方案，以访问所有客户点。

与基本VRP类似，但每个客户点有一个特定的需求量，车辆需要满足总容量限制且在不超过容量的情况下为客户提供服务。

参数：

$n$ : 客户点的数量（不包括起始点）。
$m$ : 车辆的数量。
$Q$ : 每辆车的容量限制。
$d_{i}$ : 客户点 $i$ 的需求量。
$c_{i,j}$ : 客户点 $i$ 到客户点 $j$ 的距离或成本。

变量：

$x_{ij}^k$ : 若车辆 $k$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^k$ 为1，否则为0。

目标函数：

最小化总行驶距离或成本：

$Min\\sum_{k=1}^{m}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{i,j}\\cdot x_{ij}^{k}}}}\\\\$ 约束条件：

1.每个客户点必须被访问且仅被访问一次： $\\sum_{k=1}^{m}{\\sum_{j=1}^{n}{x_{ij}^{k}}}=1,\\forall i=1,...n\\\\$

2.每辆车的路径必须从起始点开始，并在终点结束：

$\\sum_{j=1}^{n}{x_{0j}^{k}}=1,\\forall k=1,...m\\\\$

$\\sum_{i=1}^{n}{x_{i0}^{k}}=1, \\forall k=1,...m\\\\$ 3.车辆容量限制： $\\sum_{j=1}^{n}{d_{j}\\cdot x_{ij}^{k}}\\leq Q,\\forall i=1,...,n, \\forall k=1,...,m \\\\$

4.Binary(0-1)约束：

$x_{ij}^{k}\\in\\left\\{ 0,1\\right\\},\\forall i=0,...,n, \\forall j=0,...,n, \\forall k=0,...,m\\\\$ 在CVRP中，问题的目标是找到一种车辆分配方案，使得每辆车都从一个起始点开始，途中访问一系列客户点，最终返回起始点。

在基本VRP的基础上，每个客户点都有一个时间窗口，表示可以在某个时间范围内访问。目标是在满足时间窗口和车辆容量限制的情况下，最小化总行驶距离或成本。

参数：

$n$ : 客户点数量（不包括起始点）。
$m$ : 车辆数量。
$Q$ : 车辆的容量限制。
$d_{i}$ : 客户点 $i$ 的需求量。
$e_{i}$ : 客户点 $i$ 的最早开始时间。
$l_{i}$ : 客户点 $i$ 的最晚结束时间。
$c_{ij}$ : 客户点 $i$ 到客户点 $j$ 的时间或成本。

变量：

$x_{ij}^k$ : 若车辆 $k$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^k$ 为1，否则为0。
$u_{i}$ : 到达客户点 $i$ 的时间。

目标函数：

最小化总行驶距离或成本：

$Min\\sum_{k=1}^{m}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{i,j}\\cdot x_{ij}^{k}}}}\\\\$ 约束条件：

每个客户点必须被访问且仅被访问一次：

$\\sum_{k=1}^{m}{\\sum_{j=1}^{n}{x_{ij}^{k}}}=1,\\forall i=1,...n\\\\$ 2.每辆车的路径必须从起始点开始，并在终点结束：

$\\sum_{j=1}^{n}{x_{0j}^{k}}=1,\\forall k=1,...m\\\\$

$\\sum_{i=1}^{n}{x_{i0}^{k}}=1, \\forall k=1,...m\\\\$ 3.车辆容量限制：

$\\sum_{j=1}^{n}{d_{j}\\cdot x_{ij}^{k}}\\leq Q,\\forall i=1,...,n, \\forall k=1,...,m \\\\$ 4.子路径位置约束：

该约束表示，如果车辆 $k$ 从客户点 $i$ 移动到客户点 $j$ ，则到达客户点 $i$ 的时间 $u_{i}$ 必须早于到达客户点 $j$ 的时间 $u_{j}$

$u_{i}-u_{j}+(n+1)\\cdot x_{ij}^{k}\\leq n,\\forall i=1,...,n, \\forall j=2,...,n, \\forall k=1,...m\\\\$ 5.时间窗口约束:

$e_{i}\\leq u_{i}\\leq l_{i}\\\\$ 6.到达时间约束：

$u_{i}\\geq u_{j}+d_{j}+c_{ij}-M\\cdot (1- x_{ij}^{k}), \\forall i=1,...,n, \\forall j=0,...,n, \\forall k=1,...,m\\\\$ 7.Binary(0-1)约束：

$x_{ij}^{k}\\in\\left\\{ 0,1\\right\\},\\forall i=0,...,n, \\forall j=0,...,n, \\forall k=0,...,m\\\\$ 8.时间窗口和到达时间一致性：

$u_{i}\\geq e_{i}, \\forall i=1,...n\\\\ u_{i}\\leq l_{i}, \\forall i=1,...n\\\\ u_{i}\\geq 0, \\forall i=1,...n\\\\ u_{0}=0\\\\$ 该数学模型描述了车辆路径问题 with 时间窗口（VRP-TW）的数学规划形式，其中 $M$ 是一个大正数，用于线性规划中的大M法（Big-M method）来实现条件约束。

允许不同类型的车辆存在，每种类型的车辆有不同的容量和成本，目标是最小化总成本。HVRP的主要特点在于它允许在同一个问题中考虑多种不同类型的车辆，这些车辆可以有不同的容量、速度、成本等属性。因此，在解决HVRP时，需要考虑以下几个方面：

车辆类型：不同类型的车辆可能有不同的特点，如不同的容量限制、速度和成本。这些属性需要在问题中明确指定。

客户点需求：每个客户点可能需要不同数量的货物，而不同类型的车辆可以承载不同数量的货物。因此，需要确保分配到每个客户点的车辆类型满足其需求。

成本和效率：由于不同类型的车辆有不同的成本和速度，需要综合考虑成本和效率来优化路线分配。

路径优化：在HVRP中，需要找到一种分配方案，使得每个客户点都得到服务，同时最小化总行驶距离或成本。涉及到路径规划和车辆调度的问题。

数学建模：针对HVRP，需要建立适当的数学模型，考虑车辆类型、容量约束、时间窗口等因素，将问题转化为数学规划问题。混合两类车辆路径问题建模的示例如下：

参数：

$n$ : 客户点数量（不包括起始点）。
$m_1$ : 第一种车辆的数量。
$m_2$ : 第二种车辆的数量。
$Q_1$ : 第一种车辆的容量限制。
$Q_2$ : 第二种车辆的容量限制。
$d_i$ : 客户点 $i$ 的需求量。
$v_1$ : 第一种车辆的速度。
$v_2$ : 第二种车辆的速度。
$c_{ij}^{k}$ : 车辆 $k$ 由客户点 $i$ 到客户点 $j$ 的时间或成本。

变量：

$x_{ij}^{k_1}$ : 若第一种车辆 $k_1$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^{k_1}$ 为1，否则为0。
$x_{ij}^{k_2}$ : 若第二种车辆 $k_2$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^{k_2}$ 为1，否则为0。
$u_i$ : 到达客户点 $i$ 的时间。

目标函数：

最小化总行驶时间或成本：

$Min\\sum_{k_1=1}^{m_1}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{ij}^{k_1}\\cdot x_{ij}^{k_1}}}}+\\sum_{k_2=1}^{m_2}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{ij}^{k_2}\\cdot x_{ij}^{k_2}}}}\\\\$ 约束条件： 与标准的车辆路径问题类似，需要考虑每个客户点的访问次数、每辆车的起始和终止、容量限制、路径位置约束、时间窗口约束以及到达时间约束等。

补充约束： 对于不同类型的车辆，还需要引入适用于容量和速度的额外约束，以确保每种车辆类型的限制得到满足。在车辆路径问题中，可以根据具体的应用场景和问题描述，将速度 $v$ 纳入到路径成本的计算中。一般来说，路径成本可以用以下方式表示：

$c_{ij}^{k_1}=\\frac{d_{ij}}{v_1}\\\\c_{ij}^{k_2}=\\frac{d_{ij}}{v_2}\\\\$ 这个简化的数学模型描述了混合车辆路径问题的基本结构，其中涵盖了两种不同类型的车辆。实际问题中，还可能涉及更多车辆类型和复杂的约束。解决HVRP需要根据问题的具体特点进行模型建立和求解方法的选择。

考虑多个冲突的目标，如最小化总行驶距离和最小化总成本。多目标车辆路径问题（Multi-Objective Vehicle Routing Problem，MOVRP）是车辆路径问题的一种变体，其主要特点是在优化过程中考虑多个目标函数，而不仅仅是单一的目标。MOVRP涉及在满足车辆容量和其他约束条件的前提下，同时优化多个不同的目标，如最小化总行驶距离、最小化总成本、最小化车辆数量等。

MOVRP的主要挑战在于寻找一种解决方案，能够在多个不同目标之间找到一个平衡，并得到一组最优或非劣解（Pareto最优解）。这些解代表了在多个目标之间的权衡选择，没有一个解在所有目标上都优于其他解。

解决MOVRP的方法包括：

多目标优化算法：一些专门针对多目标问题的优化算法可以应用于MOVRP，例如多目标遗传算法、多目标粒子群算法、多目标模拟退火等。这些算法能够搜索并生成一组不同权衡的解。

权衡法：在某些情况下，可以使用权衡法来将多个目标函数线性组合成单一的目标函数，然后将问题转化为单一目标优化问题。这样可以使用单目标优化方法求解，但需要根据问题的需求和权重设置来确定适当的组合。

非劣排序：对于MOVRP，非劣排序技术可以用来识别和维护一组非劣解。通过比较解集中的不同解，可以构建出帕累托前沿，即一组在不同目标下都无法进一步优化的解。

参考点方法：这种方法将目标函数的值转化为相对于某个参考点的偏离程度，从而将多目标问题转化为单一目标问题。

多目标车辆路径问题（Multi-Objective Vehicle Routing Problem，MOVRP）的数学建模可以通过引入多个目标函数来表示。

以下是一个简化的MOVRP数学模型示例，假设有两个目标函数：最小化总行驶距离和最小化总成本。实际问题中可以根据需要添加更多的目标函数。

参数：

$n$ : 客户点数量（不包括起始点）。
$m$ : 车辆数量。
$Q$ : 车辆的容量限制。
$d_i$ : 客户点 $i$ 的需求量。
$c_{ij}$ : 客户点 $i$ 到客户点 $j$ 的距离。
$f_1$ : 表示行驶距离的权重因子。
$f_2$ : 表示成本的权重因子。

变量：

$x_{ij}^k$ : 若车辆 $k$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^k$ 为1，否则为0。
$u_i$ : 到达客户点 $i$ 的时间。

目标函数：

最小化多个目标函数的加权和：

$Minf_1\\cdot\\sum_{k=1}^{m}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{c_{ij}\\cdot x_{ij}^{k}}}}+f_2\\cdot\\sum_{k=1}^{m}{\\sum_{i=0}^{n}{\\sum_{j=0}^{n}{成本相关项\\cdot x_{ij}^{k}}}}\\\\$ 其中 "成本相关项" 表示成本与路径相关的函数，例如基于距离、时间、车辆类型等的成本计算。

约束条件：

每个客户点必须被访问且仅被访问一次：

$\\sum_{k=1}^{m}{\\sum_{j=1}^{n}{x_{ij}^{k}}}=1,\\forall i=1,...n\\\\$ 2.每辆车的路径必须从起始点开始，并在终点结束：

$\\sum_{j=1}^{n}{x_{0j}^{k}}=1,\\forall k=1,...m\\\\$

$\\sum_{i=1}^{n}{x_{i0}^{k}}=1, \\forall k=1,...m\\\\$ 3.车辆容量限制：

$\\sum_{j=1}^{n}{d_{j}\\cdot x_{ij}^{k}}\\leq Q,\\forall i=1,...,n, \\forall k=1,...,m \\\\$ 4.子路径位置约束：

该约束表示，如果车辆 $k$ 从客户点 $i$ 移动到客户点 $j$ ，则到达客户点 $i$ 的时间 $u_{i}$ 必须早于到达客户点 $j$ 的时间 $u_{j}$

$u_{i}-u_{j}+(n+1)\\cdot x_{ij}^{k}\\leq n,\\forall i=1,...,n, \\forall j=2,...,n, \\forall k=1,...m\\\\$ 5.时间窗口约束:

$e_{i}\\leq u_{i}\\leq l_{i}\\\\$ 6.到达时间约束：

$u_{i}\\geq u_{j}+d_{j}+c_{ij}-M\\cdot (1- x_{ij}^{k}), \\forall i=1,...,n, \\forall j=0,...,n, \\forall k=1,...,m\\\\$ 7.Binary(0-1)约束：

$x_{ij}^{k}\\in\\left\\{ 0,1\\right\\},\\forall i=0,...,n, \\forall j=0,...,n, \\forall k=0,...,m\\\\$ 8.时间窗口和到达时间一致性：

$u_{i}\\geq e_{i}, \\forall i=1,...n\\\\ u_{i}\\leq l_{i}, \\forall i=1,...n\\\\ u_{i}\\geq 0, \\forall i=1,...n\\\\ u_{0}=0\\\\$ 该模型中，通过引入权重因子 $f_1$ 和 $f_2$ ，可以对行驶距离和成本进行权衡。该模型描述了多目标车辆路径问题，可以根据问题的具体要求进行扩展和调整。

考虑客户点的需求和位置在不断变化的情况下，实时地规划车辆路径。动态车辆路径问题（Dynamic Vehicle Routing Problem，DVRP）是车辆路径问题的一种变体，考虑了实时变化的情况，其中客户需求和路况随着时间的推移而发生变化。与传统的车辆路径问题不同，DVRP要求在已经开始执行路线的情况下，根据实时信息和变化的需求进行实时的路径优化调整。

DVRP的主要特点包括：

动态需求：客户的需求在运输过程中可能发生变化，例如有新的客户加入、已有客户的需求发生变化等。

实时信息：路况可能随着时间的推移而发生变化，交通堵塞或道路封闭可能会影响路径选择。

即时调整：在DVRP中，需要根据实时信息对已经计划好的路径进行调整，以适应变化的需求和路况。

决策时机：在DVRP中，需要决定何时对路径进行调整，以在满足约束条件的情况下优化路径。

以下是一个简化的DVRP数学模型，用于描述问题的基本结构。实际问题中可能更为复杂，需要根据实际情况进行扩展和调整。

参数：

$n$ : 客户点数量（不包括起始点）。
$m$ : 车辆数量。
$Q$ : 车辆的容量限制。
$d_i$ : 客户点 $i$ 的初始需求量。
$c_{ij}$ : 客户点 $i$ 到客户点 $j$ 的距离。
$r_{ij}$ : 客户点 $i$ 到客户点 $j$ 的实时距离。
$t$ : 当前时间。
$e_i$ : 客户点 $i$ 的最早开始时间。
$l_i$ : 客户点 $i$ 的最晚结束时间。

变量：

$x_{ij}^k$ : 若车辆 $k$ 在访问客户点 $i$ 后移动到客户点 $j$ ，则 $x_{ij}^k$ 为1，否则为0。
$u_i$ :到达客户点 $i$ 的实际时间。

目标函数： DVRP通常需要在实时情况下进行路径调整，因此目标函数可能涉及路径成本和需求变化的成本等。

约束条件：

每个客户点必须被访问且仅被访问一次：

$\\sum_{k=1}^{m}{\\sum_{j=1}^{n}{x_{ij}^{k}}}=1,\\forall i=1,...n\\\\$ 2.每辆车的路径必须从起始点开始，并在终点结束：

$\\sum_{j=1}^{n}{x_{0j}^{k}}=1,\\forall k=1,...m\\\\$

$\\sum_{i=1}^{n}{x_{i0}^{k}}=1, \\forall k=1,...m\\\\$ 3.车辆容量限制：

$\\sum_{j=1}^{n}{d_{j}\\cdot x_{ij}^{k}}\\leq Q,\\forall i=1,...,n, \\forall k=1,...,m \\\\$ 4.子路径位置约束：

该约束表示，如果车辆 $k$ 从客户点 $i$ 移动到客户点 $j$ ，则到达客户点 $i$ 的时间 $u_{i}$ 必须早于到达客户点 $j$ 的时间 $u_{j}$

$u_{i}-u_{j}+(n+1)\\cdot x_{ij}^{k}\\leq n,\\forall i=1,...,n, \\forall j=2,...,n, \\forall k=1,...m\\\\$ 5.时间窗口约束:

$e_{i}\\leq u_{i}\\leq l_{i}\\\\$ 6.实时到达时间约束：

$u_{i}\\geq u_{j}+d_{j}+r_{ij}-M\\cdot (1- x_{ij}^{k}), \\forall i=1,...,n, \\forall j=0,...,n, \\forall k=1,...,m\\\\$ 7.Binary(0-1)约束：

$x_{ij}^{k}\\in\\left\\{ 0,1\\right\\},\\forall i=0,...,n, \\forall j=0,...,n, \\forall k=0,...,m\\\\$ 8.时间窗口和实时到达时间一致性：

$u_{i}\\geq e_{i}, \\forall i=1,...n\\\\ u_{i}\\leq l_{i}, \\forall i=1,...n\\\\ u_{i}\\geq 0, \\forall i=1,...n\\\\ u_{0}=t\\\\$ 该模型中，实时信息和需求变化通过实时距离 $r_{ij}$ 体现，而目标函数和约束条件的形式则取决于问题的具体情况。这是一个简化的数学模型，实际问题中需要考虑更多的因素和约束条件。

数学建模中，通常使用大M法（Big-M method）来表示条件约束，其中 $M$ 是一个大正数，用于将条件约束转化为线性规划中的约束。 $M$ 的取值需要根据具体问题的特点和约束来确定，它应该足够大以确保约束在问题的可行解范围内成立，但又不能太大以避免对最优解产生影响。

在上述数学模型中， $M$ 出现在实际到达时间约束的部分，其中用于确保约束在某些条件下成立。在这个情境中， $M$ 的取值应该足够大，以确保约束不会受到实际到达时间的限制，从而使该约束对优化问题没有影响。

具体来说， $M$ 的取值应该满足以下两个条件：

（1） $M$ 应该足够大，以确保 $u_i \\geq u_j + d_j + r_{ij}$ 这个约束在所有情况下成立。也就是说，无论实际到达时间 $u_i$ 和 $u_j$ 是多少，以及路径之间的距离 $r_{ij}$ 是多少，约束都不会被违反。

（2）同时， $M$ 不应该过大，以避免对最优解产生不必要的影响。过大的 $M$ 值可能会导致线性规划问题的数值稳定性问题或求解困难。

在实际应用中，通常需要根据问题的规模和特点，通过经验或分析来确定合适的 $M$ 值。选取适当的 $M$ 值是数学建模中的一个关键环节，需要在保证约束成立的前提下，尽可能减小 $M$ 对问题求解的影响。

上一篇：Pytorch使用Scaler时关于scheduler和optimizer顺序的报错：`optimizer.step()` before `lr_scheduler.step()`

下一篇：去哪个国家留学最容易

首页

天顺平台

天顺注册

天顺登录

天顺新闻

天顺代理加盟

关于天顺娱乐

天顺平台

天顺注册

天顺登录

天顺新闻

联系我们